在高中數學範圍中，組合是一門重要的課題，它涵蓋了排列與組合的各種公式和應用。理解這些公式對準備學術考試和未來數學學習都是必不可少的；然而，面對大量數學問題時，找到一些有效的方法可以大大提高解題效率。本文將探討在不完全相異物的概念下，組合公式中的一些方法。
 

不完全相異物的概念

在高中數學中，不完全相異物是指一組物件中有些彼此相同，有些不同。這個概念在處理實際問題時尤為重要，因為許多情況下我們需要考慮多個相同物品的排列和組合方式。例如，字母排列問題中可能出現重複字母，這時我們就需要考慮不完全相異物的情況。
 

公式的應用

 

排列與組合的基本公式

首先我們需要了解基本的排列與組合公式：

• 排列公式：從 m 個物件中選擇 n 個物件進行排列，公式為 P(m, n) = m! / (m-n)!
• 組合公式：從 m 個物件中選擇 n 個物件進行組合，公式為 C(m, n) = m! / [n!(m-n)!]

 

不盡相異物的理解與公式解析

當考慮不盡相異物時，我們需要調整基本排列公式。例如，考慮 n 個物件中有 分別p個物件是相同而另q個物件是相同的且恰n=p+q，那麼排列數量P應為：

• P= n! / p!*q!

這個公式的推導基於每個重複物件的排列數量需要被除去，因為它們的排列不會產生新的結果。
 

具體例子

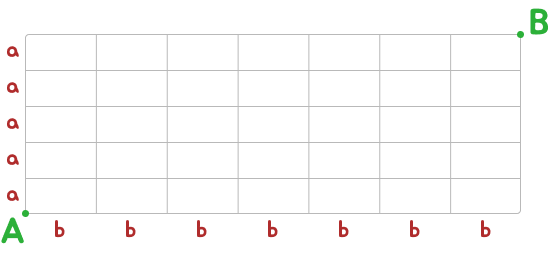
Q：如上圖，要從A點走到B點只能向右跟向上走捷徑，走法有幾種？
A：我們可以看到，它垂直的路徑總共要走5段，水平的路徑總共要走7段。不管怎麼走一定要恰恰好符合【5段垂直+7段水平】合計共12段。
從另外一個角度來看，如果把他看成是5個a跟7個b做排列，那麼不同的排列方式就會形成一個新的路徑。所以只要用不盡相異物排列的算法就可以算出總路徑數P：
P= (a+b)! / a!*b! 其中a=5,  b=7 ,a+b=12
則 
P=12!/5!*7!    
 

單元複習：重複組合的處理

排列組合中有幾種類型同學很容易混淆，以本文前半段所提到的不完全相異物的排列，可能有一部分的同學會跟重複組合或重複組合混在一起，所以我們今天先稍微提一下重複組合：
類似地，對於重複組合，我們使用以下公式來計算：

• C' = (m + n - 1)! / [n!(m-1)!]

這一公式用於計算包括重複物件的組合數量。
 

具體例子

為了說明以上公式的應用，讓我們考慮一個具體例子：

Q：考慮一個有 7 個字母的單詞，其中包含 2 個 A、3 個 B 和 2 個 C。要求計算所有不同排列的數量。
A：根據重複排列公式，我們得出：

• P' = 7! / (2! * 3! * 2!) = 5040 / (2 * 6 * 2) = 210

因此，這個單詞可以有 210 種不同的排列方式。

文章複習：戰勝排列組合（一）如何計算組合數C(m, n)：從概念到實作，搞懂C的算法！
 

學測好幫手！思無敵線上學習平台

STOODY思無敵雲端教育平台，是同學們複習學測的好幫手，我們有許多經驗豐富的老師與完整的教材，只要在線上就可以解決同學們在排列組合方面的學習問題。
在高中數學範圍內，理解並靈活應用組合公式中的各種類型，特別是在不完全相異物的情況下，把類型分清楚，可以有效地提升解題效率。通過掌握重複排列和重複組合的處理方法，我們能夠更高效地解決涉及重複物件的數學問題。希望本文所述的概念和技巧能夠為學生們提供有價值的參考，幫助他們在數學學習中取得更好的成績。